Around the Bases

I was bothered by a prompt concerning our number system. Why is this base 10, with 9 distinct symbols, system of counting the one in practice today? After some initial research, I found many other systems that seem just good. What could make one system better than another? How would the nature of mathematics have changed given a different system in place? Let's go through some of the history and make sense of how and why we count to ten.

The Babylonians 3100 BC: A base 60 system? seems absurd right? 
The Babylonian numeral system is credited as being the first positional numeral system. This means the symbol, and its position determined the value. A milestone in human history. We still see the effect this new development on time. 60 seconds in a minute, 60 minutes in an hour, however not exactly the same. Since arithmetic for large number, and powers of numbers in this system were not easy, it is no wonder it didn't survive. I look at this and see that calculations would be similar to that of Z[60].

The Egyptian Numerals 3000 BC: aha, a base 10 system.

Value	1	10	100	1,000	10,000	100,000	1 million, or many
Hieroglyph						or

The difference here being that position didnt matter. However, surprisingly, by 1740BCE, the egyptians had developed a symbol for zero. They thought of this as a baseline and eventually thought of numerals as either positive and negative. Also, they even had symbols for fractions,  a huge contribution to how our base 10 numeral system works today.

The Maya numerals: 

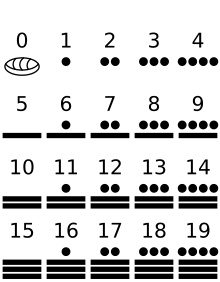
A base twenty system in which 5 dots make a bar, and numbers after 19 were written vertically as powers of twenty like so:

400s
20s
1s
	33	429	5125

So, their place holders were of vertical orientation. The use of bars and dots made arithmetic very straight forward. The Maya numeral system is most famous for its appearance in the Long Count Calendar. Our numeral system today doesn't reflect much of genius system the Maya used, however their use of zero rivaled that of their predecessors. 

The Roman Numerals 1000BC: Probably the most well known historic system of counting since some small applications using the roman numerals still exist today.

Symbol	Value
I	1
V	5
X	10
L	50
C	100
D	500
M	1,000

Surprisingly, this system did not have a 0. So the idea of negative numbers did not exist. Further, instead of writing out 4 I's, like IIII, the Romans used a sort of subtraction like IV, which we would say 5 minus 1 today. Aside from still using the Roman Numerals for basic applications like numbering lists, or telling time, the system was outclassed by another for it's ease of arithmetic and basic operations.

In a sense, the most widely used numbering system today, the Arabic numeral system, was not invented overnight. The Babylonians told us position matters. 61 is certainly different than 16 in our system. The Egyptians had a base ten for ease of application into multiplication and division, ours is also a base ten. The Maya had a base twenty, but knew that higher mathematics required very large numbers, something the Arabic systems also handles well. And the Roman Numerals, well... they are a special breed, much like the Chinese counting rods. These are used as special, or ceremonial techniques. This may be because they look nice, and can be detailed to show such special meaning.

It's was Fibonacci's famous book, Liber Abaci, that changed the way people described quantitative elements. As Fibonacci traveled the Mediterranean, he fell in love with a number system popular with Hindu and Arabic merchants.  The Hindu Arabic numeral system was born and Fibonacci set out to make it known to the world. In his book, he provided detailed instructions on how to convert from another system to the HA system, along with providing details on how to use this system in everyday applications like weight, money, and other quantities. He followed up with a second section on business, which helped economies grow. 

The role of our number system today: One thing I notice different about our modern day system is the decimal system. Of course, with a lot of work, any of the above systems could make numbers as big as they like,  but our system can handle values as small as we like. The role of our number system is especially important in application of very small numbers; like in chemistry or physics. In my opinion, the system we have today opened the door for the exploration into the hard sciences which in turn lead to a more advanced, technological civilization. However, scientist and researchers are still coming up with better number systems as the development of computer science field progresses. Traditionally, a binary system, 0s and 1s, is used in computer programming. However, some claim other systems, like that with base 16, can provide better programming and data storage. Who knows, maybe with the next 25 years we will be counting to VI (16) instead of 10.

History of Mathematics

The Greeks and Proof Writing.

Throughout my mathematical career and my experiences with proof writing, I'm convinced the Greek mathematician like Thales, Euclid, and Pythagorean made the one of the biggest contributions to communicating in mathematics. Before the Greeks, civilizations like the Egyptians and Babylonians relied on repeated observations which is what we now call inductive reasoning. The Greeks however, not only gave us geometrical theorems, but also dabbed in number theory as well as formalizing the proof process.

First, a conjecture is proposed and any mathematician will admit to trying lots and lots of examples. Sometimes, these examples will lay the groundwork for how the proof will flow. Other times, the actual proof is so abstract that even the simplest of examples can be troublesome to construct. Nevertheless, if the conjecture or proposition is proved using arbitrary elements of the given set following the axioms, then it becomes a theorem. Theorems laid by the Greeks are still in practice today. In my mind, theorems are like shortcuts; once someone has proved that the theorem holds, we can skips all steps in between and cut to the chase if we are given a problem with the same hypothesis. For example, a theorem may start out with "suppose we have a right triangle, then..."; already this grants us many avenues in which to work with the triangle since there are many theorems pertaining to right triangles.

Over the years, proof writing has become an art form. This may be because of Thales and his proof by picture. With explanation, a picture is a powerful tool. However, this limits one to thinking abstractly. Maybe that was his way of convincing his counterparts that he was right. Euclid was famous for Euclid's lemma and other number theory problems but he also made of compilation of the work of famous mathematicians that came before him. This collection was probably the most influential piece of literature for other mathematicians that came after Euclid.

All in all, the Greeks contribution to proof writing has evolved mathematics into a more diverse field.

What is Math?

What is Math?

When the general discussion of Mathematics gets started, which is always the case when peers ask me what my major is, the result quite often follows the same routine: "Oh, so you must be really good at multiplying and adding?" No, I am not a calculator. This usually goes on for several minutes before I mention studies in Abstract Algebra like Group theory or Ring theory. Math is much more than just numbers, it can be used theoretically to answer some of worlds most unexplainable phenomenon. We are in the age of information where researchers and engineers are making breakthroughs everyday using advanced computes powered by mathematical formulas and theories. From the first recipes using quantitative measurements, to the millions of lines of code in a program to predict weather, math has evolved to shape civilization and the way we see the world around us.

Mathematics can be seen everywhere in everyday life, even back to the stone age. For example, humans were probably using algebra before it had an official name. How many deer must we kill in order to feed the clan of 100 members for one week when each person eats one-eighth of a deer a week. The advancement of Algebra made it possible to predict, plan, and concur the extreme living conditions of early man. On the other hand, some of mans greatest accomplishments were possible because of Geometry. Pyramids can be found all over the world and the great pyramids in Egypt required more geometry and algebra than meets the eye. Without Calculus, Physics and advanced Statistics would not be possible. Each milestone is similar to a building block. Down the timeline, each block is built upon another supporting the overall structure. Like our human civilization, mathematics will continue to grow and evolve.